Anyone doing any type of coding has encountered transformations. They are the building block of any 3d application/game engine...
Now most of the time people will also not write their matrix code, it's already provided by any library, which ideally will provide you nice SIMD version for operations.
I assume you already know what is a Transform and what is a multiply.
So now a few operators of interest (eg: that you want to avoid to use), are Multiply (you will need it a lot but you want to save as many as you can) , and Invert (since it involves precision issue).
Generally you'll have spent a lot of time finding a reasonably fast Matrix multiply algorithm (which is SSE optimized), but then you can also simply spend time to just check how Matrix operator works and avoid using it :)
So let's take a few examples:
You can create a Translation Matrix, create a Scaling Matrix, and multiply both of them.
Now you can see there's not much point doing that, you can just set the Row for the translation and set the diagonal for the scaling. You saved one multiply just by doing this.
So here we scale by S, then translate by T
We can do the same as before, eg:
Create Scaling Matrix , Create Translation Matrix and multiply them. Again lot of operators wasted.
You can simply set diagonal to S, and set last row (Translation) to S*T.
You just multiplied two vectors component wise instead of a full matrix multiplication.
Now, if you need to translate a Matrix but you don't know what the previous Matrix contains, you would say that you need to multiply. Yes and No ....
Translating a matrix will ONLY affect the last row, so instead of having the code :
Multiply Source * Translation Matrix, you can simply have a method that applies the matrix multiplication on the last row only (eg: you do 1/4th of the operation). First three rows will not be changed, no point of processing them.
Now most of the time people will also not write their matrix code, it's already provided by any library, which ideally will provide you nice SIMD version for operations.
I assume you already know what is a Transform and what is a multiply.
So now a few operators of interest (eg: that you want to avoid to use), are Multiply (you will need it a lot but you want to save as many as you can) , and Invert (since it involves precision issue).
Generally you'll have spent a lot of time finding a reasonably fast Matrix multiply algorithm (which is SSE optimized), but then you can also simply spend time to just check how Matrix operator works and avoid using it :)
So let's take a few examples:
1/Translate and Scale
So let's say you want to move an object, then scale it.You can create a Translation Matrix, create a Scaling Matrix, and multiply both of them.
Now you can see there's not much point doing that, you can just set the Row for the translation and set the diagonal for the scaling. You saved one multiply just by doing this.
2/Scale then Translate
Now you obviously know that order or operation is important when dealing with operators, So if you scale before translate then you need a multiply.
We can do the same as before, eg:
Create Scaling Matrix , Create Translation Matrix and multiply them. Again lot of operators wasted.
You can simply set diagonal to S, and set last row (Translation) to S*T.
You just multiplied two vectors component wise instead of a full matrix multiplication.
Now, if you need to translate a Matrix but you don't know what the previous Matrix contains, you would say that you need to multiply. Yes and No ....
Translating a matrix will ONLY affect the last row, so instead of having the code :
Multiply Source * Translation Matrix, you can simply have a method that applies the matrix multiplication on the last row only (eg: you do 1/4th of the operation). First three rows will not be changed, no point of processing them.
3/Rotation
Now you have a nice rotation matrix around, but at some point you need to invert it (to process some billboards for example).
If your rotation is "pure rotation" (eg: no scaling component), this has an interesting property:
A*At = I (eg: matrix * transposed matrix) = identity.
This means that instead of inverting your matrix, you can simply transpose it for the same result, saving some multiplies).
4/Scaling
Another common operation is to scale a matrix (as per the Translate then Scale example).
So in this case you want to scale your matrix by sx,sy,sz
You can (as usual), create a scaling matrix and multiply all your lot, or simply
Multiply row 1 by sx
Multiply row 2 by sy
Multiply row 3 by sz
Et voila, 12 multiplies and you're sorted. (This can also be very easily vectorized).
5/LookAt
Look at matrix is a bit of a special transform, of course widely used for cameras.
Simply put, from 3 components:
Eye : Eye Position
Target : Position where you look at (not direction)
Up Vector : This is often used for camera Roll. (in most cases it will be 0,1,0)
From those 3 vectors you construct a matrix that brings object into a space relative to the camera.
There's no Scaling involved, so you mostly have a translation and a rotation.
Here is formula for LookAt : http://msdn.microsoft.com/en-us/library/windows/desktop/bb205342(v=vs.85).aspx
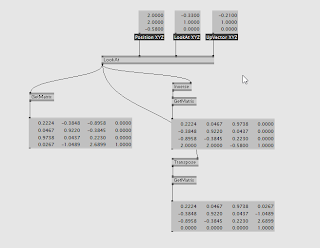
Now most times you will compute your LookAt matrix and immediately Invert it (so you can use it for sprites, deferred rendering....)
Now let's think about the translation component.
I mentioned before that a LookAt transform brings your object into camera space, so to invert it, your translation component is ... your eye position :)
Now I also mentioned that there's a rotation component, which can be extracted into a 3x3 matrix , and you can simply transpose this matrix to have the invert rotation.
So technically you can build both LookAt and Invert in one go, saving again an Inversion.
Please note that for brevity I only bothered to show the transposed part in the Patch, but you get the concept.
That's it for now, but you have much more tricks like this when dealing with vectors.
As an exercise, for the reader build projection matrix and it's inverse in one go:
Ortho : http://msdn.microsoft.com/en-us/library/windows/desktop/bb205347(v=vs.85).aspx
Perspective : http://msdn.microsoft.com/en-us/library/bb205350(v=vs.85).aspx
Have fun !
Ortho : http://msdn.microsoft.com/en-us/library/windows/desktop/bb205347(v=vs.85).aspx
Perspective : http://msdn.microsoft.com/en-us/library/bb205350(v=vs.85).aspx
Have fun !



No comments:
Post a Comment